179. Покажите, что при очень малом параметре вырождения распределения Бозе—Эйнштейна и Ферми—Дирака переходят в распределение Максвелла—Болыдмана.
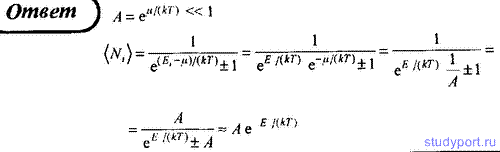
182. Объясните, при каких условиях можно применять статистику Максвелла—Больцмана к электронам в металле. Пользуясь распределением Ферми—Дирака, получите распределение Максвелла—Больцмана.
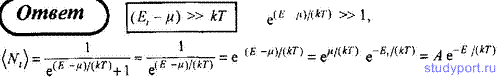
183. Определите функцию распределения для электронов, находящихся на энергетическом уровне E для случая E - EF << kT, пользуясь: 1) статистикой Ферми — Дирака; 2) статистикой Максвелла — Больцмана.

184. Определите функцию распределения Ферми—Дирака при T ≠ 0 К для электронов, находящихся на уровне Ферми. Объясните полученный результат.
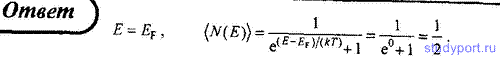
187. Определите число свободных электронов, занимающих в среднем уровень энергии, равной энергии Ферми.

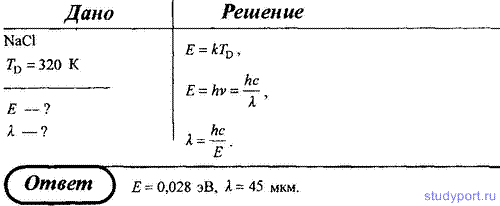
191. Определите в электрон-вольтах максимальную энергию Е фонона, который может возбуждаться в кристалле NaCl, характеризуемом температурой Дебая TD = 320 К. Фотон какой длины волны λ обладал бы такой энергией?