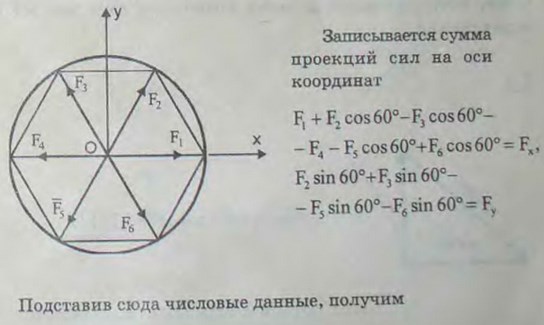
2.1 (2.1). В центре правильного шестиугольника приложены силы 1, 3, 5, 7, 9 и 11 Н, направленные к его вершинам. Найти величину и направление равнодействующей и уравновешивающей.
Ответ: 12 Н; направление уравновешивающей противоположно направлению заданной силы в 9 Н.
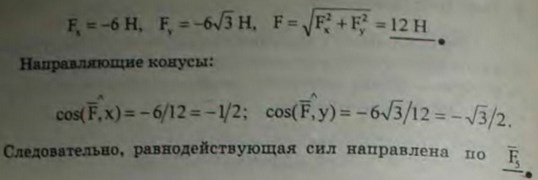
2.2(2.3). Силу в 8 Н разложить на две по 5 Н каждая. Можно ли ту же силу разложить на две по 10 Н, 15 Н, 20 Н и т. д.? На две по 100 Н?
Ответ: Да, если не заданы направления разложения.
2.3(2.4). По направлению стропильной ноги, наклоненной к горизонту под углом α = 45°, действует сила Q = 2,5 кН. Какое усилие S возникает при этом по направлению горизонтальной затяжки и какая сила N действует на стену по отвесному направлению?
Ответ: S = N = 1,77 кН.
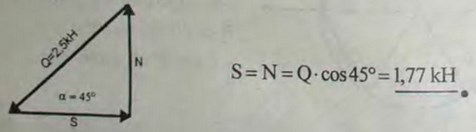
2.4(2.5). Два трактора, идущих по берегам прямого канала с постоянной скоростью, тянут барку при помощи двух канатов. Силы натяжения канатов равны 0,8 кН и 0,96 кН; угол между ними равен 60°. Найти сопротивление воды Р, испытываемое баркой при ее движении, и углы α иβ, которые должны составлять канаты с берегами канала, если барка движется параллельно берегам.
Ответ: Р = 1,53 кН, α = 33°, β = 27°.

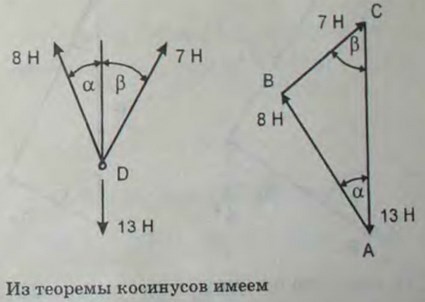
2.5(2.6). Кольца А, В и С трех пружинных весов укреплены неподвижно на горизонтальной доске. К крючкам весов привязаны три веревки, которые натянуты и связаны в один узел D. Показания весов: 8, 7 и 13 Н. Определить углы α иβ, образуемые направлениями веревок, как указано на рисунке.
Ответ: α = 27,8°, β = 32,2°.
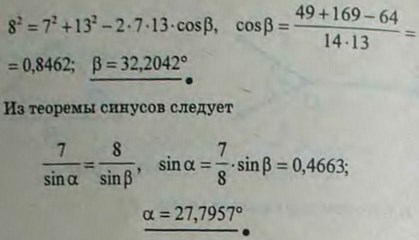
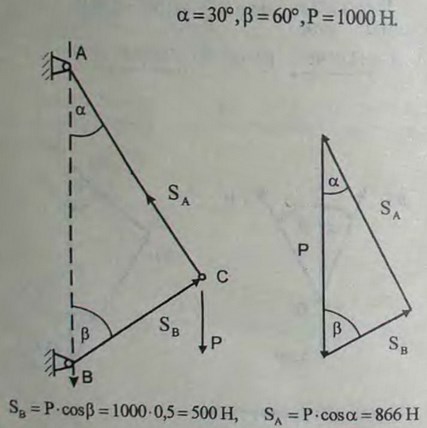
2.6(2.7). Стержни АС и ВС соединены между собой и с вертикальной стеной посредством шарниров. На шарнирный болт С действует вертикальная сила Р = 1000 Н.
Определить реакции этих стержней на шарнирный болт С, если углы, составляемые стержнями со стеной, равны: α = 30° и β = 60°.
Ответ: 866 Н, 500 Н.
2.7(2.8). На рисунках а, б и в, как и в предыдущей задаче, схематически изображены стержни, соединенные между собой, с потолком и стенами посредством шарниров. К шарнирным болтам В, F и К подвешены грузы Q = 1000 Н.
Определить усилия в стержнях для случаев:
а) α = β = 45°;
б) α = 30°, β = 60°;
в) α = 60°,β = 30°.
Ответ: a) S1 = S2 = 707 Н;
б) S1 =577 Н; S2 = -1154 Н (знак минус показывает, что стержень сжат);
в)S1 = -577 Н; S2 = 1154 Н.

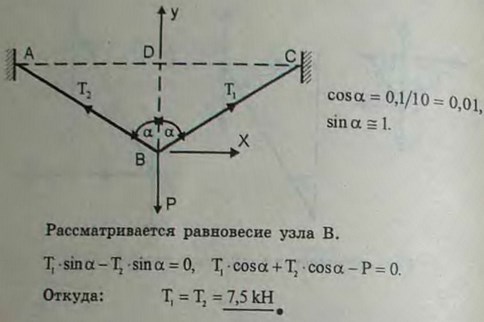
2.8(2.9). Уличный фонарь подвешен в точке В к середине троса АВС, прикрепленного концами к крюкам А и С, находящимся на одной горизонтали. Определить натяжения T1 и T2 в частях троса АВ и ВС, если вес фонаря равен 150 Н, длина всего троса АВС равна 20 м и отклонение точки его подвеса от горизонтали BD = 0,1 м. Весом троса пренебречь.
Ответ: Т1 = Т2 = 7,5 кН.
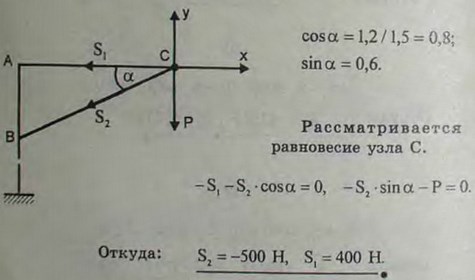
2.9(2.10). Уличный фонарь веса 300 Н подвешен к вертикальному столбу с помощью горизонтальной поперечины АС = 1,2 м и подкоса ВС =1,5 м. Найти усилия S1 и S2 в стержнях АС и ВС, считая крепления в точках А, В и С шарнирными.
Ответ: S1 = 400 Н, S2 = -500 Н.
2.10(2.11). Электрическая лампа веса 20 Н подвешена к потолку на шнуре АВ и затем оттянута к стене веревкой ВС. Определить натяжения: ТА шнура АВ и ТС веревки ВС, если известно, что угол α = 60°, а угол β = 135°. Весом шнура и веревки пренебречь.
Ответ: Та = 14,6 Н, ТС = 10,4 Н.
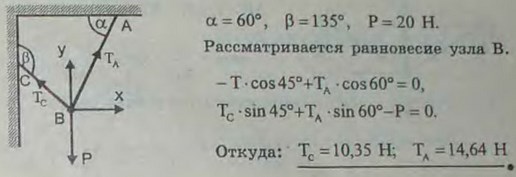
2.11(2.12). Мачтовый кран состоит из стрелы АВ, прикрепленной шарниром А к мачте, и цепи СВ. К концу В стрелы подвешен груз Р = 2 кН; углы ВАС = 15°, АСВ = 135°. Определить натяжение Т цепи СВ и усилие Q в стреле АВ.
Ответ: Т = 1,04 кН; Q = 2,83 кН.
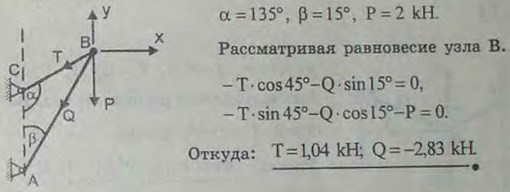
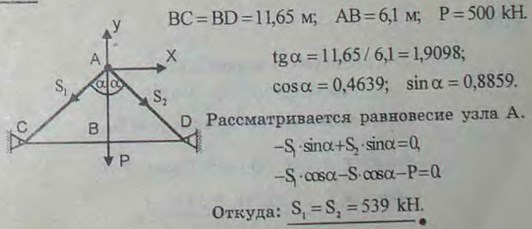
2.12(2.13). На одной железной дороге, проведенной в горах, участок пути в ущелье подвешен так, как показано на рисунке. Предполагая подвеску АВ нагруженной силой Р = 500 кН, найти усилия в стержнях АС и AD.
Ответ: Стержни АС и AD сжаты одинаковым усилием 539 кН.
2.13(2.14). Через два блока А и В, находящихся на одной горизонтальной прямой АВ = l, перекинута веревка CAEBD. К концам С и D веревки подвешены гири веса р каждая, а к точке Е — гиря веса Р. Определить, пренебрегая трением на блоках и их размерами, расстояние х точки Е от прямой АВ в положении равновесия. Весом веревки пренебречь.
Ответ: х = Pl/(2ν(4p2-p2))

2.14(2.15). Груз веса 25 Н удерживается в равновесии двумя веревками, перекинутыми через блоки и натягиваемыми грузами. Один из этих грузов весит 20 Н; синус угла, образуемого соответствующей веревкой с вертикалью, равен 0,6. Пренебрегая трением на блоках, определить величину р второго груза и угол α, образуемый второй веревкой с вертикальной линией. Весом веревки пренебречь.
Ответ: р = 15 Н, sin α = 0,8.
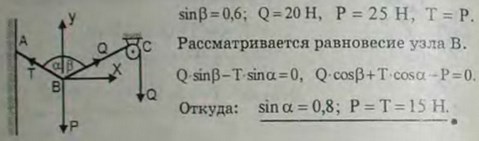
2.15(2.16). К веревке АВ, один конец которой закреплен в точке А, привязаны в точке В груз Р и веревка BCD, перекинутая через блок; к концу ее D привязана гиря Q веса 100 Н. Определить, пренебрегая трением на блоке, натяжение Т веревки АВ и величину груза Р, если в положении равновесия углы, образуемые веревками с вертикалью BE, равны: α = 45°, β = 60°.
Ответ. Т = 122 Н, Р = 137 Н.

2.16(2.17). Груз Р = 20 кН поднимается магазинным краном ВАС посредством цепи, перекинутой через блок А и через блок D, который укреплен на стене так, что угол CAD = 30°. Углы между стержнями крана: АВС = 60°, АСВ = 30°. Определить усилия Q1 и Q2 в стержнях АВ и АС.
Ответ: Q1 = 0, Q2 = —34,6 кН.

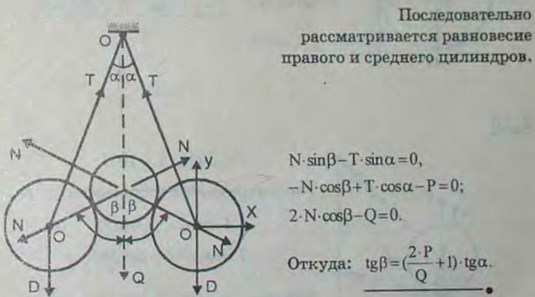
2.17. Два одинаковых цилиндра I веса Р каждый подвешены на нитях к точке О. Между ними лежит цилиндр II веса Q. Вся система находится в равновесии. Цилиндры I не касаются другдруга. Определить зависимость между углом α, образованным нитью с вертикалью, и углом β, образованным прямой, проходящей через оси цилиндров I и II, с вертикалью.
Ответ: tg β = (2P/Q+1) tg α.
2.18(2.18). На двух взаимно перпендикулярных гладких наклонных плоскостях АВ и ВС лежит однородный шар O веса 60 Н. Определить давление шара на каждую плоскость, зная, что плоскость ВС составляет с горизонтом угол 60°.
Ответ. ND = 52 Н, NE = 30 Н.
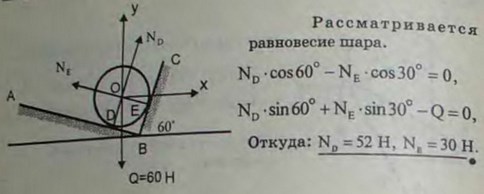
2.19(2.19). К вертикальной гладкой стене АВ подвешен на тросе АС однородный шар О. Трос составляет со стеной угол α, вес шара Р. Определить натяжение троса Т и давление Q шара на стену.
Ответ: Т = Р/cos α, Q = Р tg α.

2.20(2.20). Однородный шар веса 20 Н удерживается на гладкой наклонной плоскости тросом, который привязан к пружинным весам, укрепленным над плоскостью; показание пружинных весов 10 Н. Угол наклона плоскости к горизонту равен 30°. Определить угол α, составляемый направлением троса с вертикалью, и давление Q шара на плоскость. Весом пружинных весов пренебречь.
Ответ: α = 60°, Q = 17,3 Н.


