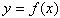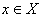, 
(X- область определения) называется множество точек этой плоскости с координатами , где .Для построения графика нужно изобразить на плоскости множество точек, координаты которых (x;y) связаны соотношением
.Чаще всего графиком функции является некоторая кривая.
Самый простой способ построения графика - построение по точкам.
Составляется таблица, в которой в одной ячейке стоит значение аргумента, а в противоположной ей значение функции от этого аргумента. Затем полученные точки отмечаются на плоскости, и через них проводится кривая.
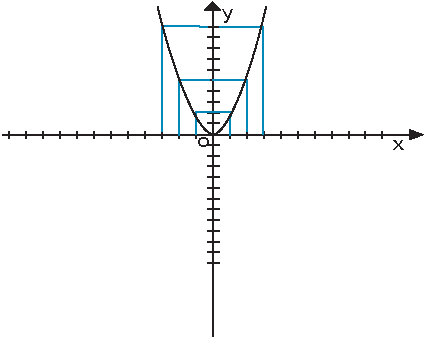
Пример построения по точкам графика функции
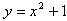:Построим таблицу.
Теперь строим график.
Но таким способом не всегда возможно построить достаточно точный график - для точности нужно брать очень много точек. Поэтому используют различные методы исследования функции.
С полной схемой исследования функции знакомятся в высших учебных заведениях. Одним из пунктов исследования функции является нахождение промежутков возрастания (убывания) функции.
Функция называется возрастающей (убывающей) на некотором промежутке, если
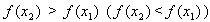, для любых x2 и x1 из этого промежутка, таких, что x2>x1.Например, функция, график которой изображен на следующем рисунке, на промежутках
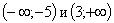возрастает, а на промежутке (-5;3) убывает. То есть, на промежутках 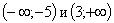график идет «в гору». А на промежутке (-5;3) «под гору».
Еще одним из пунктов исследования функции является исследование функции на периодичность.
Функция называется периодичной, если существует такое число T, что
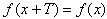.Число T называют периодом функции. Например, функция
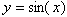периодична, здесь период равен 2П, так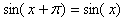 
Примеры графиков периодичных функций:
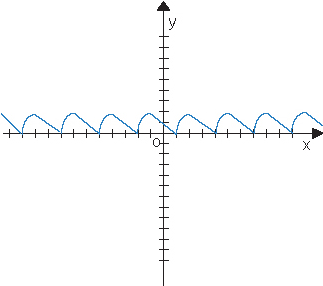
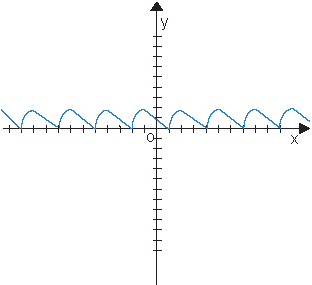
Период первой функции равен 3, а второй – 4.
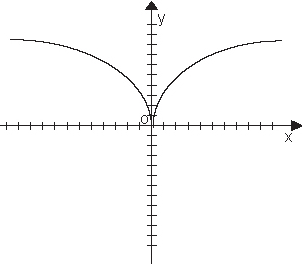
Функция называется четной, если
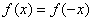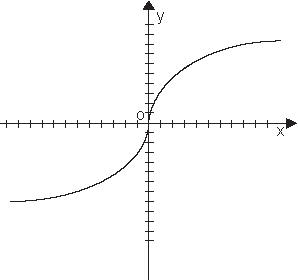
Пример четной функции y=x2.Функция называется нечетной, если
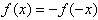Пример нечетной функции y=x3.График четной функции симметричен относительно оси ОУ (осевая симметрия).
График нечетной функции симметричен относительно начала координат (центральная симметрия).
Примеры графиков четной (слева) и нечетной (справа) функции:
