Теорема Виета:

1. Если x₁ и x₂ - корни квадратного уравнения

2. Если x₁ и x₂ удовлетворяют условиям 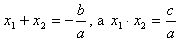, то они являются корнями квадратного уравнения.

Доказательство первого утверждения:

По формулам корней квадратного уравнения, имеем: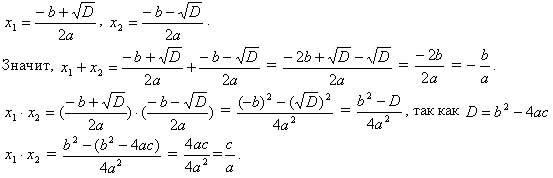



Доказательство второго утверждения:

Пусть x₁ и x₂ удовлетворяют условиям .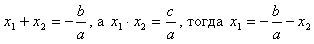

Подставим это выражение для  во второе условие, получим: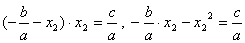



Умножим левую и правую часть, получившегося уравнения на a, имеем:

-b*x₂-ax₂²=c.

Перенесем все в правую часть:

-b*x₂-ax₂²-c=0.

Умножим левую и правую часть уравнения на -1 и поменяем местами слагаемые:

ax₂²+bx₂+c=0 - значит, x₂ является решением уравнения ax²+bx+c=0.

Аналогично докажем и для x₁.

Примеры задач, которые решаются с помощью теоремы Виета:

1. Найти коэффициенты квадратного уравнения x²+bx+c=0, если его корни равны -2 и -3.

Решение:

Используем теорему Виета 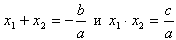. В нашем случае a=1, значит,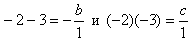



Имеем: b=5 и c=6.

Ответ: уравнение имеет вид x²+5x+6=0.

2. Найти целые корни квадратного уравнения 2x²+10x+12=0.

Решение:

Это уравнение можно конечно, решить, используя формулы корней квадратного уравнения. Но, в условии сказано, что эти корни целые, при этом , по теореме Виета .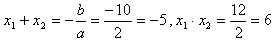

Шесть можно представить, как произведение 2*3, или (-2)*(-3), заметим, что -5=(-2)+(-3). Значит, по теореме Виета, -2 и -3 – целые корни квадратного уравнения.

Ответ: -2 и -3.