Иррациональным называется уравнение, содержащее неизвестное под знаком радикала, например,
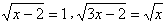 и т.д.
и т.д.
Общая схема решения иррациональных уравнений такова:
1. Избавляемся от иррациональности, возводя обе части уравнения в четную степень (при этом, возможно, предварительно будет удобно перенести какие-то слагаемые из одной части в другую и т.д.) При этом, получаем уравнение, которое не обязательно будет равносильно исходному, но множество его корней будет содержать все корни исходного.
2. Находим корни получившегося уравнения.
3. Проверяем, нет ли лишних корней, подставляя получившиеся корни в исходное уравнение. Ненужные корни убираем.
Пример:
Решить уравнение 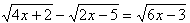 .
.
Возведем обе части уравнения в квадрат: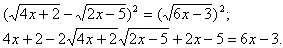
Приводим подобные: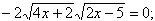
Чтобы избавиться от иррациональности, возведем в квадрат еще раз: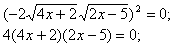
Решаем получившееся уравнение:
4x+2=0 или 2x-5=0
4x=-2 или 2x=5
x=-0,5 или x=2,5
Проверим, нет ли лишних корней: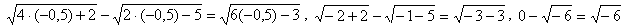 - видим, что подкоренное выражение отрицательно, значит -0,5 не удовлетворяет ОДЗ. Этот корень исключаем.
- видим, что подкоренное выражение отрицательно, значит -0,5 не удовлетворяет ОДЗ. Этот корень исключаем.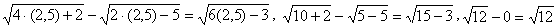 - верно, значит, этот корень берем.
- верно, значит, этот корень берем.
Ответ: 2,5

