Уравнение вида ax²+bx+c=0, где a, b, c – некоторые числа (а ? 0) называется квадратным уравнением.

Квадратное уравнение ax²+bx+c=0, при D=b²-4ac<0 действительных корней не имеет.

При D=0 имеет единственный корень 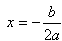(этот корень иногда называют двукратным корнем квадратного уравнения), при этом .

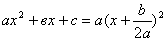При D>0 имеет два корня 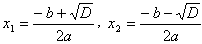при этом ax²+bx+c=a(x-x₁)(x-x₂).


Докажем эти утверждения.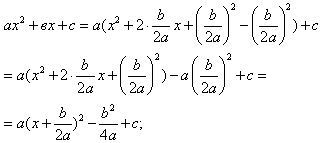


Значит, квадратное уравнение равносильно уравнению


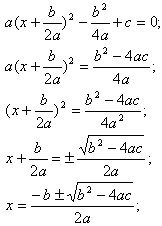
Очевидно, что это выражение не будет иметь значений в поле действительных чисел при

b²-4ac<0, и будет иметь единственное значение при b²-4ac=0.



Примеры.

1. Решить уравнение x²-8x+7=0.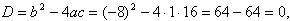


Ответ: 7, 1.



2. Решить уравнение x²-8x+16=0

D=b²-4ac=(-8)²-4*1*16=64-64=0 уравнение имеет единственное решение .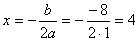



Ответ: 4.



Примечание: решение можно было найти, заметив формулу квадрата разности  и решив уравнение (x-4)²=0.



3. Решить уравнение  x²-5x+8=0

- решений в поле действительных чисел нет.