Корни уравнения ctg(x) = a выражаются формулой x=arcctg(a)+πn, n ∈ Z.

Попробуем разобраться, почему, решения выражаются этой формулой.

Проще всего это сделать, посмотрев на график функции y = ctg(x).

Корни этого уравнения – это абсциссы точек пересечения прямой y = a. Начертим на одной плоскости график функции y = ctg(x) и график функции y = a.

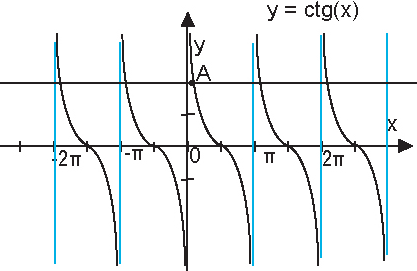
По рисунку видно, что абсцисса точки А – это arcctg(a), остальные точки пересечения имеют абсциссы x=arcctg(a)+πn, n ∈ Z.

Пример:

Решить уравнение ctg(3x) = √3.

По формуле, приведенной выше, имеем 2x = arcctg(√3)+πn, n ∈ Z.

Известно, что arcctg(√3) = π/6, значит 3x = π/6+πn, n ∈ Z, x = π/18+1/3πn, n ∈ Z.