4.1 (4.1). К однородному стержню АВ, который может вращаться вокруг шарнира А, подвешена в точке В на веревке гиря С веса в 10 Н. От конца стержня В протянут трос, перекинутый через блок D и поддерживающий гирю веса в 20 Н. Найти величину угла BAD = α, при котором стержень будет находиться в положении равновесия, зная, что АВ = AD и вес стержня 20 Н. Трением на блоке пренебречь.

Ответ: α = 120°.

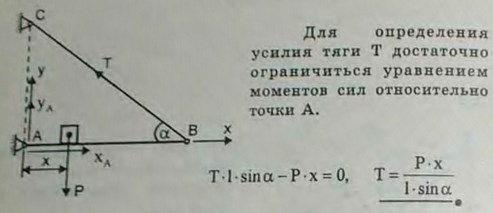
4.2(4.2). Горизонтальная балка крана, длина которой равна у одного конца укреплена шарнирно, а у другого конца В подвешена к стене посредством тяги ВС, угол наклона которой к горизонту равен α. По балке может перемещаться груз Р, положение которого определяется переменным расстоянием х до шарнира A. Определить натяжение Т тяги ВС в зависимости от положения груза. Весом балки пренебречь.

Ответ: Т = Px/(l sin α)

4.3(4.3). Однородный шар веса Q и радиуса а и гиря веса Р подвешены на веревках в точке О, как показано на рисунке. Расстояние ОМ = b. Определить, какой угол φ образует прямая ОМ с вертикалью при равновесии.

Ответ: sin φ = a/b P/(P+Q).

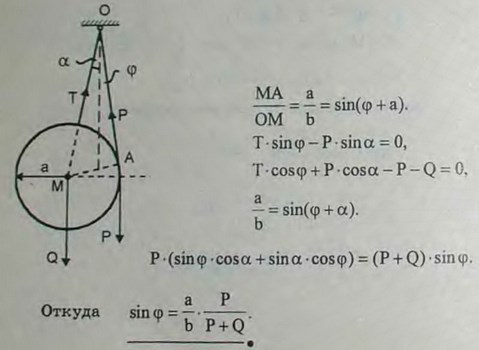
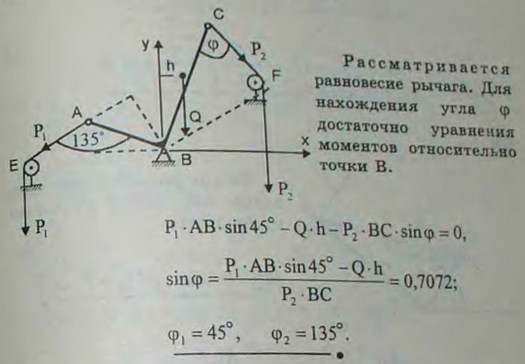
4.4(4.4). Ломаный рычаг AВС, имеющий неподвижную ось В, весит 80 Н; плечо АВ = 0,4 м, плечо ВС = 1 м, центр тяжести рычага находится на расстоянии 0,212 м от вертикальной прямой BD. В точках A и С привязаны веревки, перекинутые через блоки Е и F и натягиваемые гирями веса Р₁ = 310 Н и Р₂ = 100 Н. Пренебрегая трением на блоках, определить угол BCF = φ в положении равновесия, если угол ВАЕ = 135°.

Ответ: φ₁ = 45°, φ₂ = 135°.

4.5(4.5). Лебедка снабжена храповым колесом диаметра d₁ с собачкой А. На барабан диаметра d₂, неподвижно скрепленный с колесом, намотан трос, поддерживающий груз Q. Определить давление R на ось В собачки, если дано: Q = 50 Н, d₁ = 420 мм, d₂ = 240 мм, h = 50 мм, а = 120 мм. Весом собачки пренебречь.

Ответ: R = Qd₂/d₁ (√(a₂+h₂))/a = 31 Н.

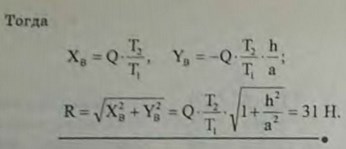
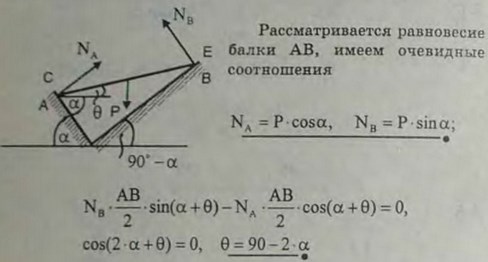
4.6(4.6). Однородная балка АВ веса Р опирается на две гладкие наклонные прямые CD и DE, находящиеся в вертикальной плоскости; угол наклона первой из них к горизонту равен α, второй: 90° - α. Найти угол θ наклона балки к горизонту в положении равновесия и давления ее на опорные прямые.

Ответ: N_A = P cos α, N_B = Р sin α, tg θ = ctg 2α, θ = 90° - 2α при а ≤ 45°.

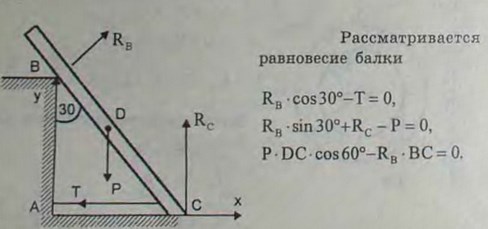
4.7(4.7). Однородная балка веса 600 Н и длины 4 м опирается одним концом на гладкий пол, а промежуточной точкой В - на столб высоты 3 м, образуя с вертикалью угол 30°. Балка удерживается в таком положении веревкой АС, протянутой по полу. Пренебрегая трением, определить натяжение веревки Т и реакции R_B столба и R_C пола.

Ответ: T = 150 Н, R_B = 173 Н, R_С = 513 Н.

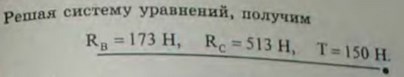
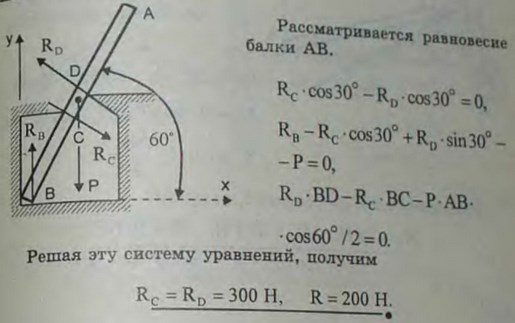
4.8(4.8). Однородная балка АВ веса 200 Н опирается на гладкий горизонтальный пол в точке В под углом 60° и, кроме того, поддерживается двумя опорами С и D. Определить реакции опор в точках В, С и D, если длина АВ = 3 м, СВ =0,5 м, BD= 1 м.

Ответ: R_B = 200 Н, R_C = 300 Н, R_D = 300 Н.

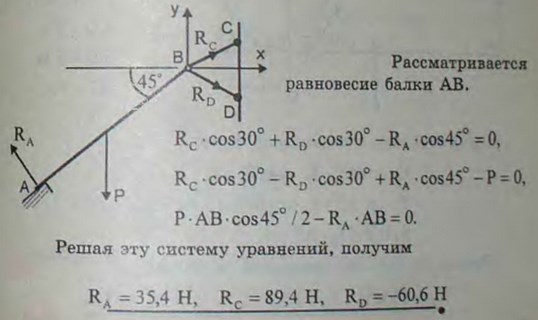
4.9(4.9). Однородная плита АВ веса Р=100 Н свободно опирается в точке А и удерживается под углом 45° к горизонту двумя стержнями ВС и BD. BCD — равносторонний треугольник. Точки С и D лежат на вертикальной прямой CD. Пренебрегая весом стержней и считая крепления в точках В, С и D шарнирными, определить реакцию опоры А и усилия в стержнях.

Ответ: R_A = 35,4 Н, S_C = 89,4 Н, S_D = -60,6 Н.

4.10(4.10). Однородный стержень АВ веса 100 Н опирается одним концом на гладкий горизонтальный пол, другим — на гладкую плоскость, наклоненную под углом 30° к горизонту. У конца В стержень поддерживается веревкой, перекинутой через блок С и несущей груз Р; часть веревки ВС параллельна наклонной плоскости. Пренебрегая трением на блоке, определить груз Р и силы давления N_A и N_B на пол и на наклонную плоскость.

Ответ: P = 25 H; N_A = 50 Н; N_B = 43,3 Н.

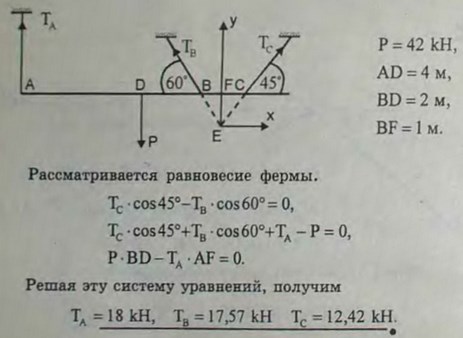
4.11(4.11). При сборке моста пришлось поднимать часть мостовой фермы АВС тремя канатами, расположенными, как указано на рисунке. Вес этой части фермы 42 кН, центр тяжести находится в точке D. Расстояния соответственно равны: AD = 4 м, DB = 2 м, BF = 1 м. Найти натяжения канатов, если прямая АС горизонтальна.

Ответ. Т_А = 18 кН, Т_в = 17,57 кН, Т_с = 12,42 кН.

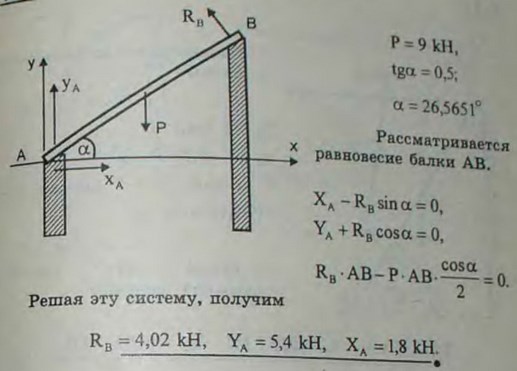
4.12(4.12). Стропила односкатной крыши состоят из бруса АВ, у верхнего конца В свободно лежащего на гладкой опоре, а нижним концом А упирающегося в стену. Наклон крыши tg α = 0,5; на брус АВ приходится вертикальная нагрузка 9 кН, приложенная в середине бруса. Определить реакции опор в точках А и В.

Ответ: X_A = 1,8 кН, Y_A = 5,4 кН, R_B = 4,02 кН.

4.13(4.13). К гладкой стене прислонена однородная лестница АВ под углом 45° к горизонту; вес лестницы 200 Н; в точке D на расстоянии, равном 1/3 длины лестницы, от нижнего конца находится человек веса 600 Н. Найти силы давления лестницы на опору A и на стену.

Ответ: Х_А = 300 Н, Y_A = 800 Н, Х_B = 300 Н.

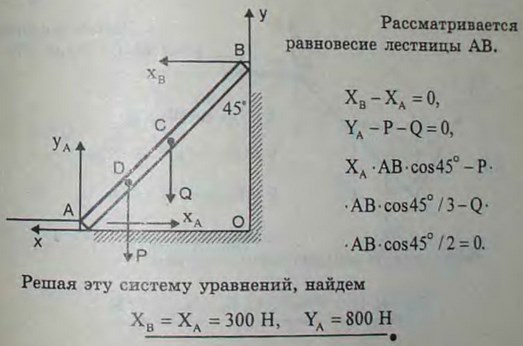
4.14(4.14). На подъемной однородной лестнице длины 6 м и веса 2,4 кН, которая может вращаться вокруг горизонтальной оси А и наклонена под углом 60° к горизонту, в точке D стоит человек веса 0,8 кН на расстоянии 2 м от конца В. У конца В лестница поддерживается веревкой ВС, наклоненной под углом 75° к горизонту. Определить натяжение Т веревки и реакцию А оси.

Ответ: Т = 3,35 кН, Х_А = 0,867 кН, Y_A = -0,0358 кН.

4.15(4.15). Однородная балка АВ веса Р = 100 Н прикреплена к стене шарниром А и удерживается под углом 45° к вертикали при помощи троса, перекинутого через блок и несущего груз G. Ветвь ВС троса образует с вертикалью угол 30°. В точке D к балке подвешен груз Q веса 200 Н. Определить вес груза G и реакцию шарнира А, пренебрегая трением на блоке, если BD = 1/4 АВ.

Ответ: G = 146 Н, X_А=73 Н, Y_A= 173,5 Н.

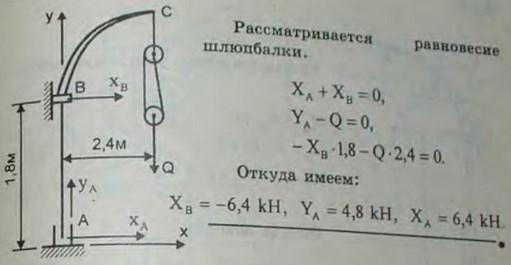
4.16(4.16). Шлюпка висит на двух шлюпбалках, причем вес ее, равный 9,6 кН, распределяется между ними поровну. Шлюпбалка АВС нижним полушаровым концом опирается на подпятник Л и на высоте 1,8 м над ним свободно проходит через подшипник В; вылет шлюпбалки равен 2,4 м. Пренебрегая весом шлюпбалки, определить силы давления ее на опоры А и В.

Ответ: Х_A = -6,4 кН, Y_A = -4,8 кН, Х_B = 6,4 кН.

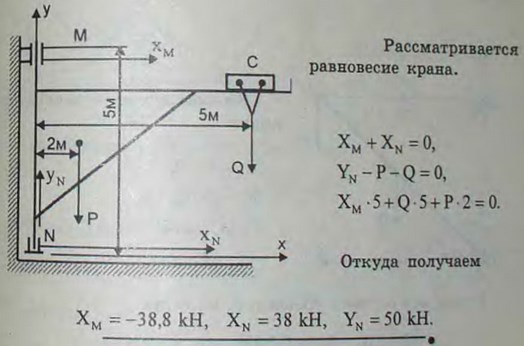
4.17(4.17). Литейный кран АВС имеет вертикальную ось вращения MN; расстояния: MN = 5 м; AС = 5 м; вес крана 20 кН, центр тяжести его D находится от оси вращения на расстоянии 2 м; вес груза, подвешенного в точке С, равен 30 кН. Найти реакции подшипника М и подпятника N.

Ответ: X_M = -38,8 кН, X_N = 38 кН, Y_N = 50 кН.

4.18(4.18). Кран в шахте, поднимающий груз Р = 40 кН, имеет подпятник A и в точке В опирается на гладкую цилиндрическую поверхность, ось которой Ay вертикальна. Длина хвоста АВ равна 2 м. Вылет крана DE = 5 м. Вес крана равен 20 кН и приложен в точке С, расстояние которой от вертикали Ay равно 2 м. Определить реакции опор A и В.

Ответ: Х_А = 120 кН, Y_А = 60 кН, Х_B = -120 кН.

4.19(4.19). Кран для подъема тяжестей состоит из балки АВ, нижний конец которой соединен со стеной шарниром A, а верхний удерживается горизонтальным тросом ВС. Определить натяжение Т троса ВС и давление на опору A, если известно, что вес груза Р = 2 кН, вес балки АВ равен 1 кН и приложен в середине балки, а угол α = 45°.

Ответ: Т = 2,5 кН, Х_А = 2,5 кН, Y_А = -3 кН.

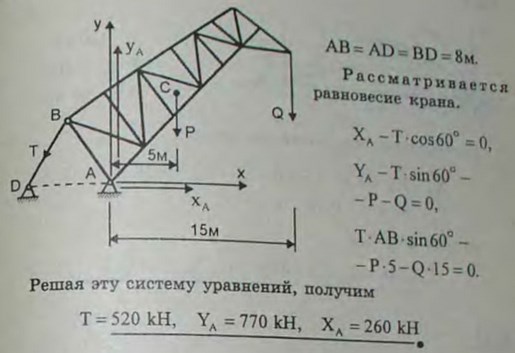
4.20(4.20). Кран имеет шарниры в точках A, В и D, причем AB = AD = BD = 8 м. Центр тяжести фермы крана находится на расстоянии 5 м от вертикали, проходящей через точку A. Вылет крана, считая от точки A, при этом равен 15 м. Поднимаемый груз весит 200 кН; вес фермы Р = 120 кН. Определить опорные реакции и натяжение стержня BD для указанного положения крана.

Ответ: Х_А = 260 кН, Y_A = 770 кН, T = 520 кН.