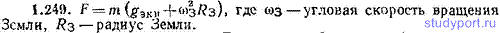1.233. Воспользовавшись значениями астрономических величин и физических констант, вычислить массу m и среднюю плотность (ρ): а) Земли, б) Солнца.
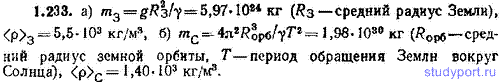
1.234. Найти силу F, с которой притягиваются друг к другу: а) Земля и Солнце, б) Луна и Земля. Сравнить эти силы.
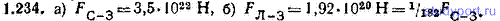
1.235. Считая, что Земля движется по круговой орбите, найти ускорение w, сообщаемое Земле Солнцем. Сравнить w c g.
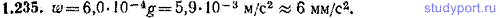
1.236. Найти первую космическую скорость v1 для Земли, т.е. скорость, которую нужно сообщить телу для того, чтобы оно стало спутником Земли.
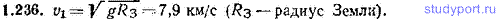
1.237. Найти вторую космическую скорость v2 для Земли, т.е. наименьшую скорость, которую надо сообщить телу для того, чтобы оно могло преодолеть действие земного притяжения и навсегда покинуть Землю. Сравнить v2 с первой космической скоростью v1.
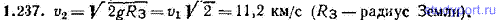
1.238. В каком случае тело удалится на большее расстояние от Земли: а) при запуске вверх по вертикали со скоростью 10 км/с или б) при запуске под углом к горизонту, равным 5°, со скоростью 12 км/с? Сопротивлением воздуха пренебречь.

1.239. Определить, при каком радиусе орбиты R (в метрах) спутник может двигаться в плоскости экватора так, чтобы все время находиться над одной и той же точкой поверхности Земли. Сравнить R с радиусом Земли R3.
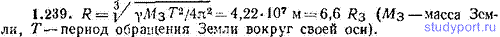
1.240. Планета движется по круговой орбите. Найти связь между радиусом орбиты R и периодом Т обращения планеты вокруг Солнца.
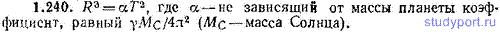
1.241. Исходя из того, что радиус земной орбиты RЗ=149,6*106 км, а радиус орбиты Марса RМ=227,8*106 км, найти период обращения Марса вокруг Солнца (выразить его в годах).

1.242. Считая Землю однородным шаром и пренебрегая вращением Земли, найти: а) ускорение свободного падения g(h) как функцию расстояния h от земной поверхности, б) значения этого ускорения для h, равных: 100, 1000, 10 000 км. Выразить найденные значения через g – ускорение вблизи поверхности Земли.
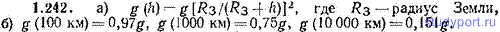
1.243. а) Найти потенциальную энергию U тела массы m, находящегося на расстоянии h от земной поверхности. Потенциальную энергию на высоте h=0 считать равной нулю. б) Получить приближенное выражение для U, справедливое при h<<RЗ (RЗ — радиус Земли).
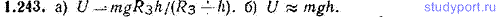
1.244. Тело запущено с поверхности Земли под углом α=45° горизонту со скоростью v0=5,20*103 м/с. Пренебрегая сопротивлением воздуха и вращением Земли, определить: а) высоту h, на которую поднимется тело над поверхностью Земли, б) скорость v тела в верхней точке траектории, в) радиус кривизны Rкр траектории в верхней точке.
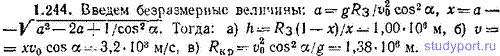
1.246. В условиях предыдущей задачи найти: а) модуль ускорения тела w(r) как функцию расстояния r от центра земного шара, б) модуль скорости тела v(r) как функцию r, в) скорость тела v(0) в момент, когда оно достигает центра Земли; сравнить v(0) с первой космической скоростью. (см. задачу 1.236), г) время τ, спустя которое тело вернется в исходную точку; сравнить τ с временем t1 за которое тело, движущееся с первой космической скоростью, облетает вокруг Земли, д) среднюю (по времени) скорость тела <v>; сравнить ее с v(0).
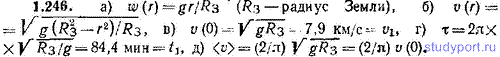
1.247. Для тела из задачи 1.245 найти: а) потенциальную энергию U{r) как функцию расстояния от центра земного шара (положить потенциальную энергию тела на бесконечно большом удалении от Земли равной нулю), б) потенциальную энергию U(0) которой обладает тело в центре Земли; сравнить U(0) с потенциальной энергией тела вблизи земной поверхности U(R).
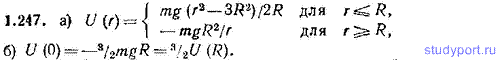
1.248. Введем вращающуюся систему отсчета, ось которой проходит через центр Солнца и перпендикулярна к плоскости земной орбиты. Система вращается в ту же сторону, что и Земля, с угловой скоростью, в два раза большей, чем скорость вращения Земли. а) Какие силы нужно учесть, рассматривая в этой системе движение Земли относительно Солнца? б) Вычислить значение и указать направление этих сил. Сравнить их с силой Fg гравитационного притяжения Земли к Солнцу.
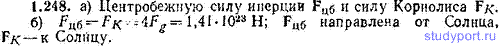
1.249. Определить силу F, с которой притягивает к себе Землю небольшое тело массы m, находящееся на экваторе недалеко от поверхности Земли. Ускорение свободного падения на экваторе считать известным и равным gэкв.